Optimized x86 assembly stuff and tricks.
Most people thinks that nowadays you can't optimize better than the compiler. This is true for most parts of your program. Some function can still be optimized with hand-crafted assembly when needed. Here you'll find some functions I've created approximations for or converted to assembly to speed them up.
Fast powf() for computation of specular intensity
Fast roundf(), floorf(), ceilf() and truncf() functions
A shufps immediate value calculator
References
- Fast powf() for computation of specular intensity:
In the phong lighting model the intensity of specular highlights is calculated using the power function a^b. Usually numbers up to 128 are used for b - the higher the exponent, the sharper/smaller the highlight.
The standard function is powf(). Here we use the famous approximation by C. Schlick [1] which is a^b ~= a / (b - a * b + a) and gets fairly close to the original.
The MSVC compiler does very well when optimizing the function in release mode, but you can still gain a bit of performance with a bit of work.
In the assembler code we get from the compiler we remove the last 2 instructions, which are redundant anyway and reorder the fld instructions which saves us a fxch.
float powf_schlick(const float a, const float b)
{
return (a / (b - a * b + a));
}
float powf_schlickASM(const float a, const float b)
{
__asm {
// floating point stack
fld dword ptr [b] // = b
fmul dword ptr [a] // = b*a
//fxch
fsubr dword ptr [b] // = b-b*a
fadd dword ptr [a] // = b-b*a+a
fdivr dword ptr [a] // = a /(b-b*a+a)
//fstp dword ptr [esp+8] // empty
//fld dword ptr [esp+8] // pow(a, b)
}
}
You can also convert this function to SSE to process floating point vectors really fast:
void powf_schlickSSE(const float * a, const float b, float * result)
{
__asm {
mov eax, a //load address of vector
movss xmm0, dword ptr [b] //load exponent into SSE register
movups xmm1, [eax] //load vector into SSE register
shufps xmm0, xmm0, 0 //shuffle b into all floats
movaps xmm2, xmm1 //duplicate vector
mov eax, result //load address of result
mulps xmm1, xmm0 //xmm1 = a*b
subps xmm0, xmm1 //xmm0 = b-a*b
addps xmm0, xmm2 //xmm2 = b-a*b+a
rcpps xmm0, xmm0 //xmm1 = 1 / (b-a*b+a)
mulps xmm2, xmm0 //xmm0 = a * (1 / (b-a*b+a))
movups [eax], xmm2 //store result
}
}
The SSE function is as fast as the single float function! By using a reciprocal and then a multiply we loose a bit of precision, but in the desired range there is no problem with that.
Here are some values measured on a Intel Pentium D 3.4GHz made with 100*10ˆ6 random numbers in the range [0,128]:
| Method |
Values |
Execution time |
Median error |
Maximum error |
| powf() |
a ε [0,1]
b ε [1,128] |
382.8ns |
0.0 |
0.0 |
| powf_schlick() |
a ε [0,1]
b ε [1,128] |
26.6ns |
< 0.01 |
˜0.2 |
| powf_schlickASM() |
a ε [0,1]
b ε [1,128] |
24.1ns |
< 0.01 |
˜0.2 |
| powf_schlickSSE() |
a ε [0,1]
b ε [1,128] |
28.8ns
(7.2ns per float) |
< 0.01 |
˜0.2 |
With my Pentium M745 (1.8GHz) the results look a bit different. The ASM method is a bit slower on that processor and the default powf() is much faster. But the SSE function is actually faster while operating on 4 floats simultaneously:
| Method |
Values |
Execution time |
Median error |
Maximum error |
| powf() |
a ε [0,1]
b ε [1,128] |
249.8ns |
0.0 |
0.0 |
| powf_schlick() |
a ε [0,1]
b ε [1,128] |
29.1ns |
< 0.01 |
˜0.2 |
| powf_schlickASM() |
a ε [0,1]
b ε [1,128] |
29.7ns |
< 0.01 |
˜0.2 |
| powf_schlickSSE() |
a ε [0,1]
b ε [1,128] |
26.8ns
(6.7ns per float) |
< 0.01 |
˜0.2 |
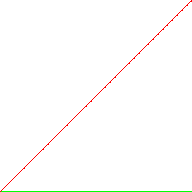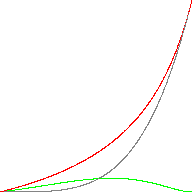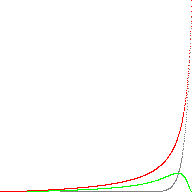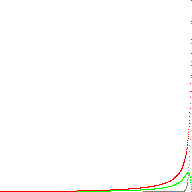
Here is an animated image comparing the real powf() (grey) to the approximation (red). The error is shown in green:
(a ε [0,1] and b ε [1, 2, 4, 8, 16, 32, 64, 128])
↑ back to top
- Fast roundf(), floorf(), ceilf() and truncf() functions:
Often you're in need of a fast floor() function for your algorithms. One way is to load a number, change the FPU control word, store the number to int and restore the original control word.
There are faster methods though. This one is from Laurent de Soras [2] and uses pure FPU code.
It rounds, floors, ceils or truncs independent of the current rounding mode. Read his PDF for the other functions and extensive information on rounding.
float floorf_ASM(const float a)
{
const float roundTowardsNI = -0.5f; //use 0.5f to round to nearest integer
float result;
__asm {
fld dword ptr [a]
fadd st, st
fadd roundTowardsNI
fistp dword ptr [result]
//return float value
sar dword ptr [result], 1
fld dword ptr [result]
/*or: return int value
mov eax, dword ptr [result]
sar eax, 1
*/
}
}
float ceilf_ASM(const float a)
{
const float roundTowardsPI = -0.5f;
float result;
__asm {
fld dword ptr [a]
fadd st, st
fsubr roundTowardsPI
fistp dword ptr [result]
//return float value
sar dword ptr [result], 1
neg dword ptr [result]
fld dword ptr [result]
/*or: return int value
mov eax, dword ptr [result]
sar eax, 1
neg eax
*/
}
}
Laurent also present methods for trunc and round to nearest, but those can be done with functions already existant in SSE which are probably faster:
float trunc_SSE(const float a)
{
float result;
__asm {
cvttss2si eax, dword ptr [a]
//cvttsd2si eax, qword ptr [a] //for double values
//return float value. if you want to return an int, you're actually done already...
mov dword ptr [result], eax
fld dword ptr [result]
}
}
float round_SSE(const float a)
{
float result;
__asm {
cvtss2si eax, dword ptr [a] //round according to rounding control bits in the MXCSR register
//cvtsd2si eax, qword ptr [a] //for double values
//return float value. if you want to return an int, you're actually done already...
mov dword ptr [result], eax
fld dword ptr [result]
}
}
Another trunc variant comes with SSE3, which has its own FPU instruction for this purpose and might be faster in some scenarios:
float trunc_SSE3(const float a)
{
float result;
__asm {
fld dword ptr [a]
fisttp dword ptr [result]
//fisttp qword ptr [result] //for double values
//return float value
fld dword ptr [result]
/*or: return int value
mov eax, dword ptr [result]
*/
}
}
Sadly I have no timing values yet...
↑ back to top
- A shufps immediate value calculator
The shupfs instruction always annoys the hell out of me. You need it often, but I usually get the immediate value wrong though I know how it works.
Or when reading some SSE code I always have to figure out what goes where...
Use the combo boxes or change the text field value to see the results.
| source |
3 |
2 |
1 |
0 |
| | |
| destination |
3 |
2 |
1 |
0 |
|
shufps destination, source, 0x |
|
| | | | | | | |
| destination |
|
|
|
|
| | |
The great line drawing JavaScript is from p01. Thanks a lot man!
↑ back to top
|



































